Question

A group of boys and girls were surveyed on their favorite football team. 5 more boys favored the Giants compared to the girls. A total of 33 boys and girls were surveyed. How many boys liked the Giants and how many girls liked the Giants?

Answer 1

Answer: 14 girls and 19 boys

Explanation:

We know that the total number of boys and girls is 33 that like the Giants, and we know that the number of boys is 5 units bigger than the number of girls, then we have 2 equations:

If we define b as the number of boys and g as the number of girls.

b + g = 33

b = g + 5

We can replace the second equation into the first:

g + 5 + g = 33

2g + 5 = 33

2g = 33 - 5 = 28

g = 28/2 = 14

So we have a total of 14 girls and we know that b = g + 5 = 14 + 5 = 19

So there are 19 boys

Answer 2

Answer: 19 boys and 14 girls liked the Giants.

Explanation:

Let be "b" the number of boys who liked the Giants and "g" the number of girls who liked the Giants.

Based on the information given, set up a system of equations:

`\left \{ {{b+g=33} \atop {b=g+5}} \right.`

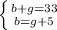
Use the Substitution method to solve this system of equations.

First, you must substitute the second equation in the first equation and solve for "g":

`(g+5)+g=33\\\\2g=33-5\\\\g=(28)/(2)\\\\g=14`

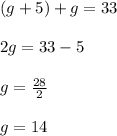
And finally, you must substitute the value of "g" into the second equation in order to find the value of "b".

Then:

`b=(14)+5\\\\b=19`