Question

A satellite is in a 91.0 min period circular orbit 330 km above Earth's surface. A)Find the satellite's speed.

B)Find its centripetal acceleration.

Answer 1

Step-by-step explanation:

It is given that,

The satellite is placed 330 km above Earth's surface, r' = 330 km

The radius of the Earth, R = 6,371 km

Time period of the satellite, T = 91 min = 5460 seconds

So, the radius of satellite,
`r=(330+6371)\ km=6701* 10^3\ m`

(A) The speed of the satellite is given by :

`v=(2\pi r)/(T)`

`v=(2\pi * 6701* 10^3)/(5460)`

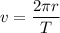
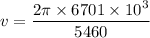
v = 7711.28 m/s

(B) The centripetal acceleration is given by :

`a=(v^2)/(r)`

`a=((7711.28)^2)/(6701* 10^3)`

`a=8.87\ m/s^2`

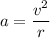
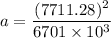
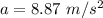
Hence, this is the required solution.