Step-by-step explanation:
It is given that,
An electric dipole consists of charges +2e and -2e separated by 0.82 nm
Charge,

Distance between charges,
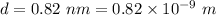
Electric field strength,
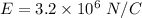
(a) The magnitude of the torque on the dipole is given by :
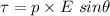
When dipole moment is parallel to the electric field,



(b) When the dipole is perpendicular to the electric field,
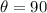

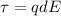 (Since, p = q × d)
(Since, p = q × d)
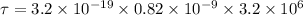
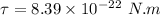
(c) When the dipole moment is anti parallel to the electric field,
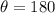
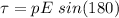
Since,
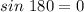

Hence, this is the required solution.