Question

A train moving with a velocity of 42.9 km/hour North, increases its speed with a uniform acceleration of 0.250 m/s^2 North until it reaches a velocity of 160.0 km/hour North. What distance did the train travel while it was increasing its velocity, in units of meters? Give the answer as a positive number

Answer 1

3658.24m

Step-by-step explanation:

Hello!

the first thing that we must be clear about is that the train moves with constant acceleration

A body that moves with constant acceleration means that it moves in "a uniformly accelerated motion", which means that if the velocity is plotted with respect to time we will find a line and its slope will be the value of the acceleration, it determines how much it changes the speed with respect to time.

When performing a mathematical demonstration, it is found that the equations that define this movement are as follows.

`\frac {Vf^(2)-Vo^2}{2.a} =X`

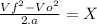
Vf = final speed =160km/h=44.4m/s

Vo = Initial speed =42.9km/h=11.92m/s

A = acceleration =0.25m/s^2

X = displacement

solving

`\frac {44.4^(2)-11.92^2}{2.(0.25)} =X\\X=3658.24m`

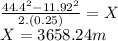
the distance traveled by the train is 3658.24m