Answer:
Part a)
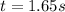
Part b)

Since the distance of other building is 15 m so YES it can make it to other building
Part c)
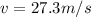
direction of velocity is given as
![[tex]\theta = 26.35 degree](https://img.qammunity.org/2020/formulas/physics/college/5f1qi3k1374w57wtt0otd0e2ivysrt1vvb.png)
Step-by-step explanation:
Part a)
acceleration due to gravity on this planet is 3/4 times the gravity on earth
So the acceleration due to gravity on this new planet is given as
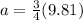
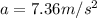
now the vertical displacement covered by the canister is given as
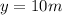
now by kinematics we have
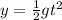
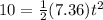
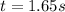
Part b)
Horizontal speed of the canister is given as

now the distance moved by it
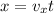
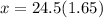

Since the distance of other building is 15 m so YES it can make it to other building
Part c)
Final velocity in X direction will remains the same

final velocity in Y direction
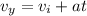

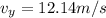
now magnitude of velocity is given as
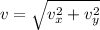

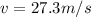
direction of velocity is given as

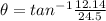
![[tex]\theta = 26.35 degree](https://img.qammunity.org/2020/formulas/physics/college/5f1qi3k1374w57wtt0otd0e2ivysrt1vvb.png)