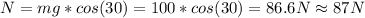Question

A100 N box sits on a 30 degree incline. The magnitude of the normal force acting on it is: a. none of these

b. 87 N
c. 100 N
d. 50 N

Answer 1

b. 87N

Step-by-step explanation:

Start by looking at the picture I attached you. As you can see in the diagram of the left, the weight=mg has one component in the x-axis and another in the y-axis. The normal force is directly over the y-axis, so we dont have to worry about the forces on the x-axis. Now, take a look at the diagram of the right, using it, we will be able to find the weight over the y-axis with trigonometry identities:

`cos(30)=(mg_y)/(mg)`

`mg_y=mg*cos(30)`

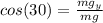
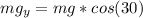
Now applying newton's second law:

`\Sigma F_y=ma`

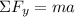
There is no acceleration in this case, so a=0

`\Sigma F_y=0\\mg*cos(30)-N=0`

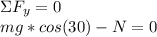
Solving for N:

`N=mg*cos(30)=100*cos(30)=86.6N\approx87N`