Question

We have a rod made of a certain metal. The rod’s length is L = 1.2 m and has a circular cross section with radius r= 3.8mm. If we hang the rod vertically and hang a mass of m = 22 kg at its end we find that it is stretched by d = 2.5 mm. (a) Using the information given, estimate the Young’s modulus for this metal rod, in N/m.

(b) If we know that this metal has a density of 12 g/cm^3, what would be the speed of sound in this metal in m/s?

Answer 1

Y = 2.286 *
`10^(9)`) N/m

V = 436.46 m/s

Step-by-step explanation:

Length, L= 1.2 m

Radius, R=3.8 mm=3.8*
`10^(-3)`

mass, m = 22 kg

Extension, ΔL = 2.5 mm

(a)

Forces P= mg =22*9.8 =215.6 N

Stress = P/A

= 215.6/[(
`\pi`(r)²]

Stress = ( 215.6 ) / [(3.14* (3.18*
`10^(-3)`)²]

Stress= 4.755 *
`10^(6)` N/m²

Strain in rod = ΔL/L = (2.5 *
`10^(-3)`)/(1.2)

=(2.08 *
`10^(-3)`)

Now, Toung midulus =Y= Stress/ Strain

=(4.755 *
`10^(6)` )/(2.08 *
`10^(-3)`)

=(2.286 *
`10^(9)`) N/m

(b)

Density of metal = 12 g/
`cm^(3)`

= 12*10³ kg/m

Speed of sound in the metal=

v=
`\sqrt{(Y)/(density) }  = \sqrt{(2.286*10^(9) )/(12*10^(3) ) }`

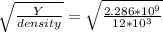
V=436.46 m/s