Question

Bonds often pay a coupon twice a year. For the valuation of bonds that make semiannual payments, the number of periods doubles, whereas the amount of cash flow decreases by half. Using the values of cash flows and number of periods, the valuation model is adjusted accordingly. Assume that a $1,000,000 par value, semiannual coupon US Treasury note with four years to maturity has a coupon rate of 3%. The yield to maturity (YTM) of the bond is 11.00%. Using this information and ignoring the other costs involved, calculate the value of the Treasury note:

Answer 1

Value of the Treasury note at 11% YTM: $ 746,617.36

Step-by-step explanation:

The present value will be sum of the future cuopon payment and maturity at market rate.

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 15,000 (1,000,000 x 3% / 2 payment per year)

time 8 (4 years x 2 payment per year)

rate 0.055 ( 11% annual / 2 payment per year)

`15000 * (1-(1+0.055)^(-8) )/(0.055) = PV\\`

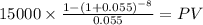
PV $95,018.4898

`(Maturity)/((1 + rate)^(time) ) = PV`

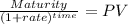
Maturity 1,000,000.00

time 8.00

rate 0.055

`(1000000)/((1 + 0.055)^(8) ) = PV`

PV 651,598.87

PV coupon $ 95,018.4898

PV maturity $ 651,598.8707

Total $ 746,617.3605