Question

Two long, charged, thin-walled, concentric cylindrical shells have radii of 4.3 and 7.0 cm. The charge per unit length is 4.8 × 10^-6 C/m on the inner shell and -6.4 × 10^-6 C/m on the outer shell. What are the (a) magnitude E and (b) direction (radially inward or outward) of the electric field at radial distance r = 6.1 cm? What are (c) E and (d) the direction at r = 12 cm?

Answer 1

(a). The electric field at r = 6.1 cm is
`1.4*10^(6)\ N/C`.

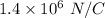(b). The direction of electric field is outward.

(c). The electric field at r = 12 cm is
`2.3*10^(5)\ N/C`.

(d). The direction of electric field is inward.

Step-by-step explanation:

Given that,

Radius of small shell = 4.3 cm

Radius of large shell = 7.0 cm

Charge per unit length inner shell
`\lambda= 4.8*10^(-6)\ C/m`

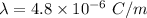
Charge per unit length outer shell
`\lambda= -6.4*10^(-6)\ C/m`

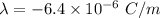
(a). We need to calculate the electric field at r = 6.1 cm

`r_(i)<r=6.1\ cm<r_(o)`

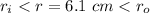
Using formula of electric field

`E(r)=(\lambda_(i))/(2\pi\epsilon_(0)r)`

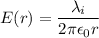
Put the value into the formula

`E_(r)=(4.8*10^(-6))/(2\pi*8.85*10^(-12)*6.1*10^(-2))`

`E_(r)=1.4*10^(6)\ N/C`

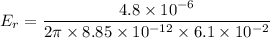
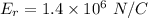
(b). We need to calculate the direction of the electric field

The direction of electric field is outward.

(c). Since,
`r>r_(o)`

We need to calculate the electric field at r = 12 cm

Using formula of electric field

`E(r)=(\lambda_(i)+\lambda_(o))/(2\pi\epsilon_(0)r)`

`E_(r)=(4.8*10^(-6)-6.4*10^(-6))/(2\pi*8.85*10^(-12)*12*10^(-2))`

`E_(r)=−2.3*10^(5)\ N/C`

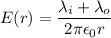
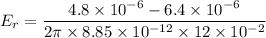
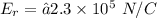
Negative sign shows the direction of electric field is inward.

(d). We need to calculate the direction of the electric field

The direction of electric field is inward.

Hence, This is the required solution.