Question

MamaMia's Pizza purchases its pizza delivery boxes from a printing supplier. MamaMia's delivers on-average 200 pizzas each month (assume deterministic demand). Boxes cost 20 cents each, and each order costs $10 to process. Because of limited storage space, the manager wants to charge inventory holding at 30 percent of the cost. The lead time is 7 days, and the restaurant is open 360 days per year, assuming 30 days per month. Determine the economic order quantity, reorder point assuming no safety stock, number of orders per year, and total annual cost.

Answer 1

Q´ = 894 pizzas per order

Reorder point r = 2.68 cycles/year

D = 2400 pizzas/year

Total annual inventory cost TAC = $53.66 per year

Step-by-step explanation:

having the following:

D = 2400 pizzas/year

Ch = ($0.2/unit)*0.3 = $0.06/unit

Co = $10/order

calculating pizza quantities in order:

Q´ = E*O*Q = ((2*D*Co)/Ch)^1/2 = ((2*2400*10)/0.06)^1/2 = 894.4 = 894 pizzas per order

calculating the reorder point:

Reorder point r = (2400 pizzas/year)*(1/894 cycles/pizza) = 2.68 cycles/year

Calculating the total annual inventory cost:

Total annual inventory cost TAC = (D*Co/Q) + ((Q/2)*Ch) = (2400*10/894) + (0.06*(894/2)) = 26.85 + 26.82 = $53.66 per year

It can be seen that when the TAC is calculated using Q´, the annual order costs are similar to the annual maintenance costs. Can be done for $0.25/unit pizza cost.

Answer 2

a) 138 units

b) 17 units

c) 17 units

d) Total Cost = $353.35

Step-by-step explanation:

Given:

Average pizzas delivered = 200

Charge of inventory holding = 30% of cost

Lead time = 7 days

Now,

a) Economic Order Quantity =
`\sqrt\frac{2*\textup{Annual Demand}*\textup{Cost per Order}}{\textup{Carrying cost}}`

also,

Annual Demand = 200 × 12 = 2400

Cost per Order = Cost of Box + Processing Costs

= 30 cents + $10

= $10.30

and, Carrying Cost =
`\frac{\textup{Total Inventory Cost}}{\textup{total annual demand}}`

=
`\frac{\textup{Total Cost per order}*\textup{Annual demand}*(25)/(100)}{\textup{Annual demand}}`

=
`\frac{\$10.30*2400}*(25)/(100)}{2400}`

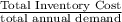
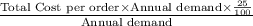
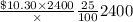
= $2.575

Therefore,

Economic Order Quantity =
`\sqrt\frac{2*\textup{2400}*\textup{10.30}}{\textup{2.575}}`

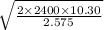
= 138.56 ≈ 138 units

b) Reorder Point

= (average daily unit sales × the lead time in days) + safety stock

= (
`(200)/(30)*7`

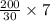
= 46.67 ≈ 47 units

c) Number of orders per year =
`\frac{\textup{Annual Demand}}{\textup{Economic order quantity}}`

=
`\frac{\textup{2400}}{\textup{138}}`

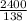
= 17.39 ≈ 17 units

d) Total Annual Cost (Total Inventory Cost)

= Ordering Cost + Holding Cost

Now,

The ordering Cost = Cost per Order × Total Number of orders per year

= $10.30 × 17

= $175.1

and,

Holding Cost = Average Inventory Held × Carrying Cost per unit

Average Inventory Held =
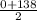`\frac{\textup{0+138}}{\textup{2}}` = 69

Carrying Cost per unit = $2.575

Holding Cost = 69 × $2.575 =

$177.675

Therefore,

Total Cost = Ordering Cost + carrying cost

= $175.1 + $177.675 = $353.35