Question

If a frog jumps with an initial velocity of 100m/s at an angle of 60°. a. What is the frog’s x and y components of velocity? b. How high will the frog get? c. How long will it take the frog to reach its maximum height?

Answer 1

Step-by-step explanation:

It is given that,

Initial velocity of frog, u = 100 m/s

It jumps at an angle of 60 degrees.

(a) Let
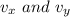`v_x\ and\ v_y` are the x and y components of velocity. It can be calculated as :

`u_x=u\ cos\theta`

`u_x=100* \ cos(60)`

`u_x=50\ m/s`

`u_y=u\ sin\theta`

`u_y=100* \ sin(60)`

`u_y=86.6\ m/s`

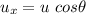
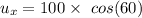
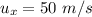
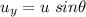
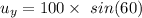
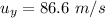
(b) Let y is the maximum height reached by the frog. It can be calculated using the third equation of motion as :

At maximum height,
`v_y=0`

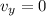
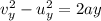`v_y^2-u_y^2=2ay` and a = -g

`-u_y^2=-2g`

`y=(u_y^2)/(2g)`

`y=(86.6^2)/(2* 9.8)`

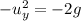
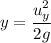
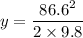
y = 382.63 meters

(c) Let t is the time taken by the frog to reach its maximum height. It can be calculated as :

`v_y=u_y-gt`

`0=u_y-gt`

`t=(u_y)/(g)`

`t=(86.6\ m/s)/(9.8\ m/s^2)`

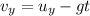
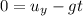
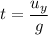
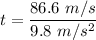
t = 8.83 seconds

Hence, this is the required solution.