Answer:
n=1.53
T₂ = 166.16 °C
Step-by-step explanation:
Given that
P₁=0.85 bar
V₁= 0.25 m³
P₂=2.8 bar
V₂=0.115 m³
Lets take compression index is n
So
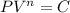
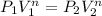
Now by putting the values
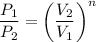
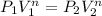
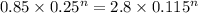
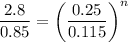
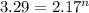
ln 3.29 = n ln 2.17
n=1.53
T₁=18°C=273+ 18 = 291 K
Lets final temperature =T₂
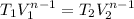
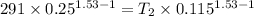
T₂=439.16 K
T₂ = 166.16 °C