Question

Kayla and her best friend Christina go shopping. The function p(t) = 2x4 + 6x3 - 3x2 + 24 represents how much money each girl spent based on the

number of hours they were shopping. If Kayla and Christina each go shopping for 2 hours, how much money did they spend together?
$44
$88
$92
$184

Answer 1

Option 4 - $184

Explanation:

Given : Kayla and her best friend Christina go shopping. The function
`p(t) = 2x^4 + 6x^3 - 3x^2 + 24` represents how much money each girl spent based on the number of hours they were shopping. If Kayla and Christina each go shopping for 2 hours.

To find : How much money did they spend together?

Solution :

The function
`p(t) = 2x^4 + 6x^3 - 3x^2 + 24`.

If Kayla and Christina each go shopping for 2 hours i.e. x=2.

`p(2) = 2(2)^4 + 6(2)^3 - 3(2)^2 + 24`

`p(2) = 32 + 48-12 + 24`

`p(2) = 92`

The total amount of money Kayla and her best friend Cristina spent together is

`Total=\$92+\$92\\\\Total=\$184`

Therefore, they spend together is $184.

So, option 4 is correct.

Answer 2

Answer: LAST OPTION.

Explanation:

You have the following function that represents the amount of money each girl spent:

`p(t) = 2x^4 + 6x^3 - 3x^2 + 24`

Where "t" is the number of hours they were shopping.

You know that each girl went shopping for 2 hours.

Then, you can substitute
`t=2` into the given function:

`p(2) = 2(2)^4 + 6(2)^3 - 3(2)^2 + 24`

Evaluating, you get that the amount of money spent by one of these girls in 2 hours, is:

`p(2) = 92`

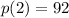
Therefore, the total amount of money Kayla and her best friend Cristina spent together is:

`Total=\$92+\$92\\\\Total=\$184`

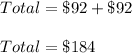
This matches with the last option.