Question

Suppose you enter into a 9-month long forward contract on a non-dividend-paying stock when the stock price is S0 = $125 and the risk-free rate is 2.0% per annum with continuous compounding. (a) What are the forward price (F0) and the initial value of the forward contract? (b) Three months later, the price of the stock (S0) is $112, and the risk-free remains 2.0%. What are the forward price (F0) and the value of the forward contract? (c) Another month later (4 months from today), the risk-free rate increases to 2.25% while the stock price stays $112.

Answer 1

Future Price

F0: 126.89

F3: 113.13

F4: 113.41

Value of the contract:

a) zero (by definition)

b) -13

c) -13

Step-by-step explanation:

forward price:

`F = S (1+r)^(n)`

being S the spot rate

time 9 months and

rate 2% continuous componding

As the rate is continuous we calculate using the e number instead:

`F = S e^(rn) +cost`

`F = 125 e^(0.02 * 9/12)`

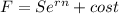
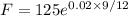
F = 125 x 1.015113065

F = 126.8891331 = 126.89

3th month into the contract:

`F = 112 e^(0.02 * 6/12)`

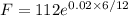
F = 113.1256187 = 113.13

4th month

`F = 112 e^(0.025 * 5/12)`

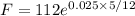
F = 113.4087866 = 113.41

value of the contract

at third month:

Vt = St - F0

Vt = 112 - 125 = -13

at fourth month

Vt = 112 - 125 = -13