Question

A hive of bees contains 27 bees when it is first discovered. After 3 days, there are 36 bees. It is determined that the population of bees increases exponentially.

How many bees are will there be after 30 days?

Answer 1

After 30 days, there will be around 542 bees in the hive.

Explanation:

Givens

• The hive contains 27 bees in first place.
• After 3 days, there are 36 bees.

The population growth is modelled by the expression

`A=A_(0)e^(kt)`

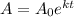
Where
`A` is the population after
`t` days,
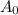`A_(0)` is the initial population,
`t` is days and
`k` is the constant of proportionality.

Basically, in these kind of problems, we use the given information to find
`k` first

`A=A_(0)e^(kt)\\36=27e^(3k)\\(36)/(27)= e^(3k)\\ln((4)/(3))=ln(e^(3k))\\3k=ln((4)/(3))\\k\approx 0.10`

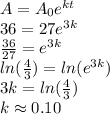
Now, with this constant, we find the population of bees after 30 days.

`A=A_(0)e^(kt)\\A=27e^(0.10(30))\\A=27e^(3)\approx 542`

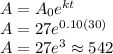
Therefore, after 30 days, there will be around 542 bees in the hive.