Question

The graph of the function f(x) = (x + 2)(x + 6) is shown below. On a coordinate plane, a parabola opens up. It goes through (negative 6, 0), has a vertex at (negative 4, negative 4), and goes through (negative 2, 0). Which statement about the function is true? The function is positive for all real values of x where x > –4. The function is negative for all real values of x where –6 < x < –2. The function is positive for all real values of x where x < –6 or x > –3. The function is negative for all real values of x where x < –2.

Answer 1

It's B in edge

Answer 2

The function is negative for all real values of x where –6 < x < –2

Explanation:

we have

`f(x)=(x+2)(x+6)`

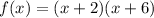
This function represent a quadratic equation (vertical parabola open upward)

The vertex represent a minimum

using a graphing tool

see the attached figure

The x-intercepts are x=-6 and x=-2

The y-intercept is the point (0,12)

The vertex is the point (-4,-4)

The domain is the interval -----> (-∞,∞) (All real numbers)

The range is the interval -----> [-4,∞) (All real numbers greater than or equal to -4)

The function is positive for x < -6 or x > -2

The function is negative for the interval (-6,-2) ----> –6 < x < –2

therefore

The function is negative for all real values of x where –6 < x < –2