Answer:
Model A=30, Model B: 20, Model C: 45
Explanation:
Let x be the amount of type A mp3 produced, and the amount of model B mp3's produced and z the amount of model C mp3 produced.
Since in total there are 303 hours for electronics work, then:
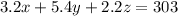
Since in total there are 393 hours for assembly, then:
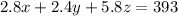
Since in total there are 416 hours for quality assurance, then:
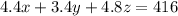
Then, the linear system associated to the problem is
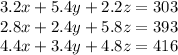
with coefficient matrix
![A=\left[\begin{array}{ccc}3.2&5.4&2.2\\2.8&2.4&5.8\\4.4&3.4&4.8\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/b9n48u30h22ysa2tyweofpoooc1q3hshbz.png) and vector of constant terms
and vector of constant terms
![b=\left[\begin{array}{ccc}303\\393\\416\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/m50kaso1igelvlzjcpnd0w7mhw5k82ebwk.png)
Since the determinant of A is equal to 36.704 then A is invertible.
Then for solve the system
 , is enough find the inverse of A and operate
, is enough find the inverse of A and operate

Using Octave we obtain that
![A^(-1)=\left[\begin{array}{ccc}-0.22&-0.50 &0.71\\0.33&0.15&-0.34\\-0.028& 0.35&-0.20\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ybvb7dzy96pam28gfnvpab1jt7e5gdax8x.png)
Then
![x=A^(-1)b=\left[\begin{array}{ccc}30\\20\\45\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/m03u2yabytuhh2x595ho2xofjlvsova9sy.png)
This means that 30 mp3's of model A, 20 of model B and 45 of model C must be produced