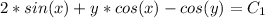Question

Find the solution of the problem (1 3. (2 cos x - y sin x)dx + (cos x + sin y)dy=0.

Answer 1

`2*sin(x)+y*cos(x)-cos(y)=C_1`

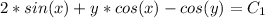
Explanation:

Let:

`P(x,y)=2*cos(x)-y*sin(x)`

`Q(x,y)=cos(x)+sin(y)`

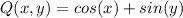
This is an exact differential equation because:

`(\partial P(x,y))/(\partial y) =-sin(x)`

`(\partial Q(x,y))/(\partial x)=-sin(x)`

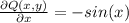
With this in mind let's define f(x,y) such that:

`(\partial f(x,y))/(\partial x)=P(x,y)`

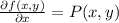
and

`(\partial f(x,y))/(\partial y)=Q(x,y)`

So, the solution will be given by f(x,y)=C1, C1=arbitrary constant

Now, integrate
`(\partial f(x,y))/(\partial x)` with respect to x in order to find f(x,y)

`f(x,y)=\int\  2*cos(x)-y*sin(x)\, dx =2*sin(x)+y*cos(x)+g(y)`

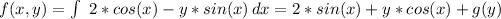
where g(y) is an arbitrary function of y

Let's differentiate f(x,y) with respect to y in order to find g(y):

`(\partial f(x,y))/(\partial y)=(\partial )/(\partial y) (2*sin(x)+y*cos(x)+g(y))=cos(x)+(dg(y))/(dy)`

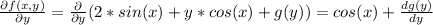
Now, let's replace the previous result into
`(\partial f(x,y))/(\partial y)=Q(x,y)` :

`cos(x)+(dg(y))/(dy)=cos(x)+sin(y)`

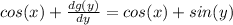
Solving for
`(dg(y))/(dy)`

`(dg(y))/(dy)=sin(y)`

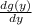
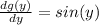
Integrating both sides with respect to y:

`g(y)=\int\ sin(y)  \, dy =-cos(y)`

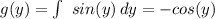
Replacing this result into f(x,y)

`f(x,y)=2*sin(x)+y*cos(x)-cos(y)`

Finally the solution is f(x,y)=C1 :

`2*sin(x)+y*cos(x)-cos(y)=C_1`