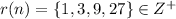Question

Over the universe of positive integers,

define p(n): n is prime and n < 32.

q(n): n is a power of 3.

r(n): n is a divisor of 27.

Please explain if possible, Thanks!

Answer 1

Answer and explanation:

Over the universe of positive integers, define the following.

The universe of discourse is
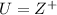`U=Z^+` i.e. set of positive integer.

`U=Z^+=\{1,2,3,4,5.....\}`

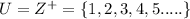
a) p(n) : n is prime and n < 32.

The set form in which all numbers are prime and less than 32.

So,
`p(n)=\{1,3,5,7,11,13,17,19,23,29,31\}\in Z^+`

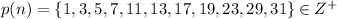
b) q(n): n is a power of 3.

The set form in which all numbers which has power of 3.

So,
`q(n)=\{3^0,3^1,3^2,3^3,3^4...\}\in Z^+`

`q(n)=\{1,3,9,27,81...\}\in Z^+`

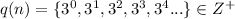
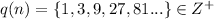
c) r(n): n is a divisor of 27.

The set form in which all numbers which is factor of 27

So,
`r(n)=\{1,3,9,27\}\in Z^+`