Question

1. Let x[n] be a signal with x[n] = 0 for n<-1 and n > 3. For each signal given below, determine the values of n for which it is guaranteed to be zero. (a) x [n -2] (b) x [n+ 3] (c) x [-n + 1]

Answer 1

a) n<1 and n>5

b) 0 < n < -4

c) n > 2 and n < -2

Explanation:

The signal is given by x[n] = 0 for n < -1 and n > 3

The problem asks us to determine the values of n for which it's guaranteed to be zero.

a) x[n-2]

We know that n -2 must be less than -1 or greater than 3.

Therefore we're going to write down our inequalities and solve for n

`n-2<-1\\n<-1+2\\n<1\\\\n-2>3\\n>5`

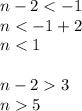
Therefore for n<1 and n>5 x [n-2] will be zero

b) x [n+ 3]

Similarly, n + 3 must be less than -1 or greater than 3

`n+3<-1\\n<-1-3\\n<-4\\\\n+3>3\\n>3-3\\n>0`

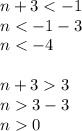
Therefore for n< -4 and n>0, in other words, for 0 < n < -4 x[n-2] will be zero

c)x [-n + 1]

Similarly, -n+1 must be less than -1 or greater than 3

`-n+1<-1\\-n<-1-1\\-n<-2\\n>2\\\\-n+1>3\\-n>3-1\\-n>2\\n<-2`

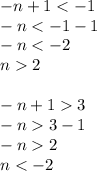
Therefore, for n > 2 and n < -2 x[-n+1] will be zero