Question

S (SOA) An annuity pays 1 at then end of each year for n years. Using an annual effective interest rate of i, the accumulated value of the annuity at time (n + 1) is 13.776. It is also known that (1 + i)* = 2.476. Calculate n. A) 4 B) 5 C) 6 D) 7 8

Answer 1

8

Explanation:

Given:

Annuity at time (n + 1) = 13.776

(1 + i)ⁿ = 2.476

Now,

`S_(n/i)=((1+i)^n-1)/(d)`

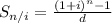
here, d =
`(i)/(1-i)`

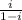
thus,

`13.776=(2.476-1)/(d)`

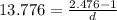
or

d = 0.1071

therefore,

d =
`(i)/(1+i)`

or

0.1071 =
`(i)/(1+i)`

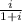
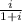
or

0.1071 + 0.1071i = i

or

i = 0.1199

now,

(1 + i)ⁿ = 2.476

or

(1 + 0.1199)ⁿ = 2.476

1.1199ⁿ = 2.476

taking log both sides

n × log(1.1199) = log(2.476)

or

n = 8.006 ≈ 8

hence,

the answer is 8