Answer:
93.75% of these surgical procedures takes at-least 80 to 160 minutes.
Explanation:
Given : Hospital records show that a certain surgical procedure takes on the average of 120 minutes with a standard deviation of 10 minutes.
To find : Between how many minutes must be the lengths of at least 93.75% of these surgical procedures?
Solution :
The average mean is
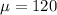 minutes.
minutes.
The standard deviation is
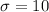 minutes.
minutes.
At least 93.75% of these surgical procedures,
Applying Chebyshev's theorem,
For any constant k>1, no more than
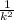 of teh data set lie outside the k standard deviations away from the mean i.e. at-least
of teh data set lie outside the k standard deviations away from the mean i.e. at-least
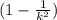 of the distribution value fall within 'k' standard deviations.
of the distribution value fall within 'k' standard deviations.
So,

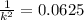
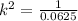
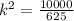
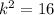
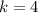
Length must be given by,
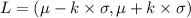

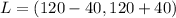
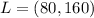
Therefore, 93.75% of these surgical procedures takes at-least 80 to 160 minutes.