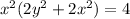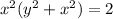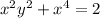Question

Solve the following IVP:

2. 2x^2 +y^2 +xyy′ =0, x>0, y(1)=1

Answer 1

`x^2y^2+x^4=2`

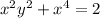
Explanation:

The given differential equation is:

`2x^2+y^2+xyy'=0,x\:>\:0,y(1)=1`

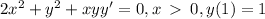
We rewrite this as

`2x^2+y^2+xy(dy)/(dx)=0,x\:>\:0,y(1)=1`

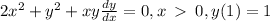
We make
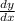`(dy)/(dx)` the subject to get:

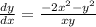`(dy)/(dx)=(-2x^2-y^2)/(xy)`....a homogeneous equation.

`(dy)/(dx)=-2((x)/(y))-((y)/(x))`

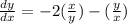
We use the following substitutions to obtain a seperable equation:

`y=vx,(dy)/(dx)=v+x(dv)/(dx),v=(y)/(x),\:and\:(1)/(v)=(x)/(y)`.

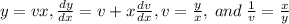This implies that:

`v+(xdv)/(dx)=(-2)/(v)-v`

`(xdv)/(dx)=(-2)/(v)-2v`

`(xdv)/(dx)=(-2-2v^2)/(v)`

`(v)/(-2-2v^2)dv=(dx)/(x)`

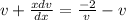
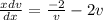
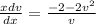
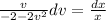
We integrate both sides to obtain:

`\int (v)/(-2-2v^2)dv=\int (dx)/(x)`

`(-\ln|2v^2+2|)/(4)=\ln x+\ln K`

`-\ln|2v^2+2|=4(\ln x+\ln K)`

`\ln ((1)/(2v^2+2))=4\ln (Kx)`

`\ln ((1)/(2v^2+2))=\ln(K^4x^4)`

`(1)/(2v^2+2)=Cx^4`

`Cx^4(2v^2+2)=1`

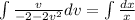
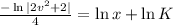
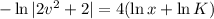
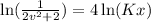
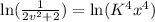
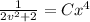
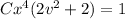
We substitute
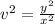`v^2=(y^2)/(x^2)` to get:

`Cx^4(2*(y^2)/(x^2)+2)=1`

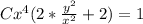
We substitute x=1,y=1 from the initial conditions.

`C(1)^4(2*(1^2)/(1^2)+2)=1`

`4C=1`

`C=(1)/(4)`

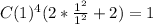
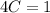
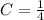
Our solution now becomes:

`x^2(2y^2+2x^2)=4`

`x^2(y^2+x^2)=2`

`x^2y^2+x^4=2`