Question

Let S = {1, 2, ...,8). How many partitions of S are there consisting of exactly two blocks, where one of the blocks has 3 elements and the other block has 5 elements? Answer. 112 Hint:

Answer 1

The total number of partitions is 56.

Explanation:

Given : Let S = {1, 2, ...,8).

To find : How many partitions of S are there consisting of exactly two blocks, where one of the blocks has 3 elements and the other block has 5 elements?

Solution :

Set S = {1, 2, ...,8)

According to question,

The first partition consists of 3 elements.

Which means 3 elements can be chosen out of 8 in
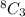`^8C_3` ways.

i.e.
`^8C_3=(8!)/(3!(8-3)!)`

`^8C_3=(8* 7* 6* 5!)/(3* 2* 1* 5!)`

`^8C_3=(8* 7* 6)/(3* 2* 1)`

`^8C_3=8* 7`

`^8C_3=56`

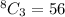
The remaining 5 elements will automatically fall into the second partition.

Therefore, the total number of partitions is 56.