Answer:
The all possible rational zeroes of f(x) are
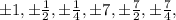
Explanation:
Consider the provided cubic function.
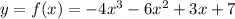
Rational zeros Theorem states that:
If P(x) is a polynomial and if p/q is a zero of P(x), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x).
Therefore,
The factor of constant term: ±1, ±7
Factors of leading coefficient: ±1, ±2, ±4
The Possible values of p/q:
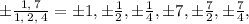
Hence, the all possible rational zeroes of f(x) are
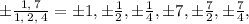
Note: These are all possible rational zeroes.
The rational zeros of the provided cubic function is x=1.
Substitute x=1 in provided function.
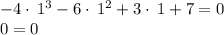
Which is true.
Hence, the rational zeros of the provided cubic function is x=1.