Question

Use a proof by contrapositive to prove that for all n E Z, n2 – 2 is not divisible by 4.

Answer 1

See explanation below.

Explanation:

To prove by contrapositive means to assume the contrapositive of what we want to prove and it should lead us to a contradiction.

So, let's assume that n²- 2 is divisible by 4

Therefore there exists a k ≥1 such that

n² - 2 = 4k

n² = 4k + 2

Case 1: Let's assume n is even.

There exists a j≥1 such that n = 2j -1

`n^(2) = 4k +2\\(2j-1)^(2) =4k + 2\\4j^(2) -4j +1 =4k +2\\4j^(2)-4j=4k+2-1\\ 4j^(2) -4j=4k-1\\4(j^(2) -j)=4k-1\\4(j^(2) -j)+1= 4k`

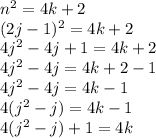
This would mean that 4 divides 1 which is a contradiction

Case 2: Let's assume n is odd

There exists a j≥1 such that n = 2j

`n^(2) = 4k +2\\ (2j)^(2) =4k +2\\ 4j^(2) -2 =4k`

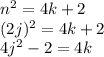
This would mean that 4 divides -2 which is a contradiction.

Therefore, we have proven that for all n ∈ Z, n²- 2 is not divisible by 4