Question

HW-02 Problem No.2.1 / 10 pas 5x1 - x2 = 1 ( 3x2 - 2x1 = -3 Solve the system of linear equations by modifying it to REF and to RREF using elementary equivalent operations. Show REF and RREF of the system. Matrices may not be used. Show all your work, do not skip steps. Displaying only the final answer is not enough to get credit. Solution (Show all intermediate steps, formulas, calculations, explanations and comments below this line. Don't write above this line)

Answer 1

`REF= \left[\begin{array}{ccc}5&-1&1\\0&(-7)/(5) &(-18)/(5)\end{array}\right]`

`RREF=\left[\begin{array}{ccc}1&0&(5)/(7) \\0&1&(18)/(7)\end{array}\right]`

Explanation:

The augmented matrix of the system is:
`\left[\begin{array}{ccc}5&-1&1\\3&-2&-3\end{array}\right]`

First we find the stepped form of A (REF):

1. We subtract 3/5 from row 1 to row 2 (R2-
`(3)/(5)`R1) and get the matrix

`\left[\begin{array}{ccc}5&-1&1\\0&(-7)/(5) &(-18)/(5)\end{array}\right]`

Note that this matrix is in echelon form.

Now we find the reduced row echelon form of the augmented matrix (RREF)

2. From the previous matrix, we multiply the first row by 1/5 and the second row by -5/7 and obtain the matrix:

`\left[\begin{array}{ccc}1&(-1)/(5) &(1)/(5) \\0&1&(18)/(7)\end{array}\right]`

3. From the previous matrix, to row 1 we add 1/5 of row 2 (R1 +
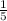`(1)/(5)`R2) and we obtain the matrix

`\left[\begin{array}{ccc}1&0&(5)/(7) \\0&1&(18)/(7)\end{array}\right]`

which is the reduced row echelon form of the augmented matrix.