Answer:
See explanation below
Explanation:
To prove by contradiction, we are going to assume that a and b are odd.
If a and b are odd, then there exists integers j, k > 0 such that
a = 2j + 1 and b= 2k + 1
We're going to rewrite the original expression substituting a and b by their odd expression.
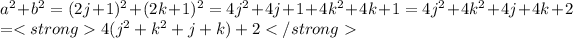
Now we have to cases, c is even or c is odd.
Case 1: If c is odd.
If c is odd, then c² is also odd, but we have that the expression above is even. Therefore, this is a contradiction.
Case 2: If c is even.
If c is even then it's multiple of 2, and c² is multiple of 4, but the expression above is not multiple of 4 (because it has the form 4g + 2). Therefore we have a contradiction.
Thus, a or b must be even.