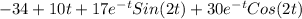Question

2. Solve the following ODEs using Laplace transforms. b. ö(t) + 2y(t) + 5y(t) = 50t – 150; y(0) = -4; $(0) = 14;

Answer 1

y(t) =
`-34+10 t + 17 e^(-t) Sin(2 t) + 30 e^(-t) Cos(2 t)`

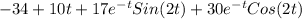
Explanation:

We use the Laplace transform in the function y''(t) +2y'(t)+ 5y(t) =50t-150

ℒ{ y''(t) +2y'(t)+ 5y(t)} =ℒ{50t-150}

ℒ{ y''(t)} +2ℒ{y'(t)}+ 5ℒ{y(t)} =ℒ{50t-ℒ{150}

s²·Y(s)-s·y(0)-y'(0)+2s·Y(s)-2·y(0)+5·Y(s)=
`(50)/(s^2)-(150)/(s)`

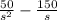
s²·Y(s)-s·(-4)-(14)+2s·Y(s)-2·(-4)+5·Y(s)=
`(50)/(s^2)-(150)/(s)`

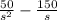
Y(s)·(s²+2s+5)+4s-14+8=
`(50)/(s^2)-(150)/(s)`

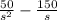
Y(s)·(s²+2s+5)=
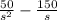`(50)/(s^2)-(150)/(s)`-4s+6

Y(s)·(s²+2s+5)=
`(50-150s-4s^3+6s^2)/(s^2)`

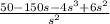
Y(s)=
`(50-150s-4s^3+6s^2)/(s^2(s^2+2s+5))`

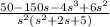
The new function can also be expressed as partials fractions:

Y(s)=
`(50-150s-4s^3+6s^2)/(s^2(s^2+2s+5))`=
`(A)/(s)+(B)/(s)+(Cs+D)/(s^2+2s+5)`

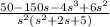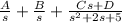
Hence,

`50-150s-4s^3+6s^2=[tex(](A)/(s)+(B)/(s^2)+(Cs+D)/(s^2+2s+5)`)×[s^2(s^2+2s+5)]

50-150s+6s²-4s³=(A+C)s³+(2A+B+D)s²+(5A+2B)s+(5B)

A+C=-4 ⇒ C=-4+34=30

2A+B+D=6 ⇒ D=64

5A+2B=-150 ⇒ A=-34

5B=50 ⇒ B=10

The function Y(s) is:

Y(s)=
`(-34)/(s)+(10)/(s^2)+(30s+64)/(s^2+2s+5)`

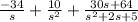
30s+64 can be expressed as:

30s+64= 30(s+1)+34

s²+2s+5 can be expressed as:

s²+2s+5=(s²+2s+1)-1+5=(s+1)²+4

Then:

Y(s)=
`(-34)/(s)+(10)/(s^2)+(30(s+1))/((s+1)^2+2^2)+(17*2)/((s+1)^2+2^2)`

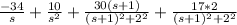
We use the inverse Laplace transform and find the transformation in the table:

ℒ⁻¹{Y(s}=ℒ⁻¹{
`(-34)/(s)+(10)/(s^2)+(30(s+1))/((s+1)^2+2^2)+(17*2)/((s+1)^2+2^2)`}

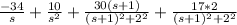y(t)=
`- 34 + 10 t + 17 e^(-t) Sin(2 t) + 30 e^(-t) Cos(2 t)`