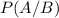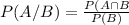Question

A teacher has found that the probability that a student studies for a test is 0.610.61​, and the probability that a student gets a good grade on a test is 0.790.79​, and the probability that both occur is 0.560.56. a. Are these events​ independent? b. Given that a student​ studies, find the probability that the student gets a good grade. c. Given that a student gets a good​ grade, find the probability that the student studied.

Answer 1

Answer with step-by-step explanation:

Let

A=Student studies for a test

B=Student gets good grade on a test

The probability that a student studies for a test=P(A)=0.61

The probability that a student gets a good grade on a test=P(B)=0.79

The probability that both occur=
`P(A\cap B)=0.56`

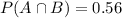
a.We have to find the events are independent

We know that if two events A and B are independent then

`P(A)\cdot P(B)=P(A\cap B)`

`P(A)\cdot P(B)=0.61* 0.79=0.4819`

`P(A\cap B)\\eq P(A)\cdot P(B)`

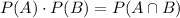
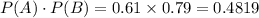
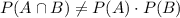
Hence, given events are not independent.

b.We have to find
`P(B/A)`

`P(B/A)=(P(A\cap B))/(P(A))`

`P(B/A)=(0.56)/(0.61)=0.92`

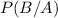
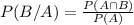
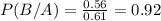
c. We have to find
`P(A/B)`

`P(A/B)=(P(A\cap B)/(P(B))`

`P(A/B)=(0.56)/(0.79)=0.71`