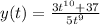Question

Solve the following initial value problem: dy +9y 6 dt with y(1) = 8 у:

Answer 1

The solution to the initial value problem is
`y(t)=(3t^(10)+37)/(5t^9)`

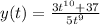
Explanation:

We have the following differential equation

`t(dy)/(dt)+9y=6t, \:{y(1)=8}`

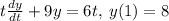
This is a linear differential equation because we can made to look like this:

`(dy)/(dt)+P(t)y=Q(t)`

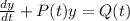
where
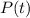`P(t)` and
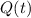`Q(t)` are functions of t.

The solution process for a first-order linear differential equation is as follows.

1. Put the differential equation in the correct initial form.

2. Find the integrating factor,
`\mu(t)`.

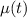3. Multiply everything in the differential equation by
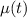`\mu(t)` and verify that the left side becomes the product rule
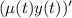`(\mu(t)y(t))'` and write it as such.

4. Integrate both sides, make sure you properly deal with the constant of integration.

5. Solve for the solution
`y(t)`.

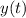Applying the solution process, we have

1. We need to get the differential equation in the correct form.

`(dy)/(dt)+(9)/(t) y=6`

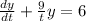
From this we can see that
`p(t)=(9)/(t)`

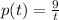
2. The integrating factor is
`\mu(t) = e^{\int {p(t)} \, dt }`

`\mu(t) = e^{\int {p(t)} \, dt }\\\mu(t) = e^{\int {(9)/(t) } \, dt }\\\mu(t) = e^(9\ln \left|t\right|)\\\mu(t) = t^9`

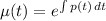
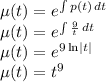
3. Now multiply all the terms in the differential equation by the integrating factor and do some simplification.

`(dy)/(dt)+(9)/(t) y=6\\t^9((dy)/(dt))+t^9((9)/(t) y)=6t^9\\(t^9y)'=6t^9`

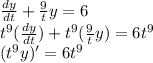
4. Integrate both sides and don't forget the constants of integration that will arise from both integrals.

`\int {(t^9y)'} \, dt =\int {6t^9} \, dt \\\\t^9 y+k=(3t^(10))/(5)+c\\\\t^9 y=(3t^(10))/(5)+c-k\\\\t^9 y=(3t^(10))/(5)+d\\\\y=(3t^(10)+5d)/(5t^9)`

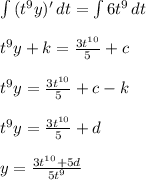
5. To find the solution we are after we need to identify the value of d that will give us the solution we are after. To do this we simply plug in the initial condition which will give us an equation we can solve for d.

`8=(3(1)^(10)+5d)/(5(1)^9) \Rightarrow d=(37)/(5)`

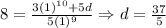
So, the actual solution to the initial value problem is

`y(t)=(3t^(10)+37)/(5t^9)`