Answer:
Expected Winnings = 2.6
Explanation:
Since the probability of rolling a 1 is 0.22 and the probability of rolling either a 1 or a 2 is 0.42, the probability of rolling only a 2 can be determined as:
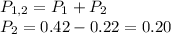
The same logic can be applied to find the probability of rolling a 3
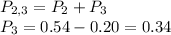
The sum of all probabilities must equal 1.00, so the probability of rolling a 4 is:
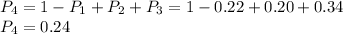
The expected winnings (EW) is found by adding the product of each value by its likelihood:
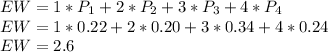
Expected Winnings = 2.6