Answer:

Explanation:
Fist the velocity of high-speed train will be given by:

And the velocity of the regular will be given by:
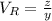
The position equations of each movement will be given by:
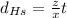
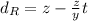
We can get the encounter point isolating t in the first equation and reepalcing it in the second one:
First isolating:
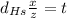
Second reeplacing t:

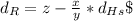
In the moment of the encounter the high-speed train have gone round
 and the regular one
and the regular one
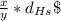
Then the difference between the distance traveled the high-speed train and the regular one is:

