Answer: 0.9088
Explanation:
Given :
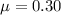
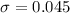
Let x be a random available that represents the proportion of students that reads below grade level .
Using
![z=\frac{x-\mu}{\sigma]() , for x= 0.36 , we have
, for x= 0.36 , we have
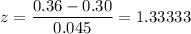
Using standard normal z-value table,
P-value
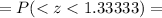
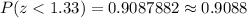 [Rounded yo the nearest 4 decimal places.]
[Rounded yo the nearest 4 decimal places.]
Hence, the probability that a second sample would be selected with a proportion less than 0.36 = 0.9088