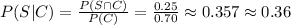Question

Suppose your friends have the following ice cream flavor preferences: 70% of your friends like chocolate (C). The remaining do not like chocolate. 40% of your friends sprinkles (S) topping. The remaining do not like sprinkles. 25% of your friends like chocolate (C) and also like sprinkles (S). If your friend had chocolate, how likely is it that they also had sprinkles? (Note: Some answers are rounded to 2 decimal places).

a. P(C)b. P(S)c. P(C and S)d. P(C | S)e. P(S | C)

Answer 1

The probability that your friend had sprinkles given that he had chocolate
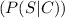`(P(S|C))` is approximately 0.357 or 0.36 if you round it to 2 decimals.

Explanation:

Let's define the following events:

C = "Your friends like chocolate flavor"

S = "Your friends like sprinkles topping"

We also know that
`P(S) = 0.7`,
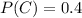`P(C) = 0.4` and
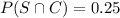`P(S \cap C) = 0.25`. We are interested in the probability of given that your friend had chocalate what is the probability that he also likes sprinkles, in other words we want
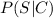`P(S|C)`. Note that,

`P(S|C) = (P(S \cap C))/(P(C)) = (0.25)/(0.70) \approx 0.357 \approx 0.36`