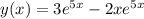Question

(15 pts) 4. Find the solution of the following initial value problem: y"-10y'+25y = 0 with y(0) = 3 and y'(0) = 13

Answer 1

`y(x)=3e^(5x)-2xe^(5x)`

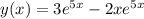
Explanation:

The given differential equation is
`y''-10y'+25y=0`

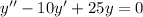
The characteristics equation is given by

`r^2-10r+25=0`

Finding the values of r

`r^2-5r-5r+25=0\\\\r(r-5)-5(r-5)=0\\\\(r-5)(r-5)=0\\\\r_(1,2)=5`

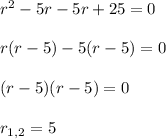
We got a repeated roots. Hence, the solution of the differential equation is given by

`y(x)=c_1e^(5x)+c_2xe^(5x)...(i)`

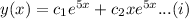
On differentiating, we get

`y'(x)=5c_1e^(5x)+5c_2xe^(5x)+c_2e^(5x)...(ii)`

Apply the initial condition y (0)= 3 in equation (i)

`3=c_1e^(0)+0\\\\c_1=3`

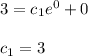
Now, apply the initial condition y' (0)= 13 in equation (ii)

`13=5(3)e^(0)+0+c_2e^(0)\\\\13=15+c_2\\\\c_2=-2`

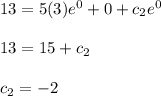
Therefore, the solution of the differential equation is

`y(x)=3e^(5x)-2xe^(5x)`