Question

A stone is dropped at t = 0. A second stone, with 5 times the mass of the first, is dropped from the same point at t = 180 ms. (a) How far below the release point is the center of mass of the two stones at t = 420 ms? (Neither stone has yet reached the ground.) (b) How fast is the center of mass of the two-stone system moving at that time?

Answer 1

a. 0.379m

b.2.646 m/s

Explanation:

Let mass of first stone=
`m_1`

Mass of second stone=
`5m_1`

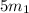
Both stones are in free fall.

The first one free fall during
`t_1=420 ms=420* 10^(-3)=0.42 s`

`1 s=1000 ms`

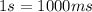
The second one free fall during
`t_2=t_1-180 ms=0.42-0.18=0.24 s`

Both stone start motion at the same point with initial velocity=0

a.We have to find the distance between the release point and below the release point where is the center of mass of the two stones.

`y=y_0+v_0t+(1)/(2)gt^2`

`y_0=0,v_0=0`

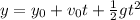
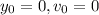
Substitute the values

`y_1=(1)/(2)(9.8)(0.42)^2=0.864 m`

`y_2=(1)/(2)* (9.8)(0.24)^2=0.282 m`

`y_(com)=(m_1y_1+m_2y_2)/(m_1+m_2)=(m_1y_1+5m_1y_2)/(m_1+5m_1)=(0.864+5(0.282))/(6)=0.379 m`

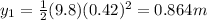
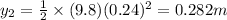
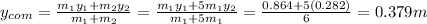
Hence, center of mass from the release point at distance=0.379 m

b.We have to find
`v_com`

`v_(com)=(m_1v_1+m_2v_2)/(m_1+m_2)`

`v_(com)=(m_1v_1+5m_1v_2)/(m_1+5m_1)=(v_1+5v_2)/(6)`

`v_1=v_01+gt=0+(9.8)(0.42)=4.116 m/s`

`v_2=v_02+gt=(9.8)(0.24)=2.352 m/s`

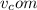
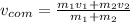
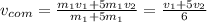
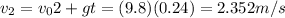
Now,
`v_(com)=(4.116+5(2.352))/(6)=2.646 m/s`