Question

David makes and sells chairs. The function p(x)=-10x^2+100x-210 indicates how much profit he makes in a month if he sells the chairs for 10-x dollars each?

Answer 1

Answer: $50 at $7 per chair

Explanation:

p(x) = -10x^2 + 100x - 210, p(9 - x) = -10(9 - x)^2 + 100(9 - x) - 210 = -10x^2 + 80x - 120 = -10(x - 2)(x - 6) x = 2, x = 6 Answer choice: B) $50 at $7 per chair

Answer 2

He makes maximum profit $40 in a month if he sells the chair for $5 each.

Explanation:

We are given that a profit function

`p(x)=-10x^2+100x-210`

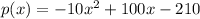
We have to find the profit he makes in a month if he sells the chair for 10-x dollar each.

`p(x)=-10(x^2-10x+21)`

`p(x)=-10(x^2-10x+25+21-25)`

`p(x)=-10((x-5)^2-4)=-10(x-5)^2+40`

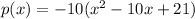
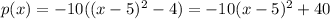
Compare with the general equation of parabola along y- axis is given by

`y=a(x-h)^2+k`

We get a=-10,h=5,k=40

The vertex of parabola is (h,k)=(5,40)

Function is maximum at vertex (5,40).

The value of x when the function is maximum

x=5

Cost of one chair=$5

Substitute the value of x=5 then we get

p(x)=
`-10(5)^2+100(5)-210=40`

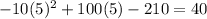
Hence, he makes maximum profit in a month $40 if he sells the chair for $5 each.