Question

A survey of athletes at a high school is conducted, and the following facts are discovered: 40% of the athletes are football players, 59% are basketball players, and 13% of the athletes play both football and basketball. An athlete is chosen at random from the high school: what is the probability that the athlete is either a football player or a basketball player? Probability = % (Please enter your answer as a percent)

Answer 1

86%

Explanation:

Let

A= Football player

B= Basket ball player

Football players=40%

Basketball players=59%

Both football and basket ball players=13%

Total percent=100%

The probability that athlete is a football player=P(A)=
`(40)/(100)=0.40`

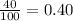
The probability that athlete is a basketball player=P(B)=
`(59)/(100)=0.59`

The probability that athlete is both basket ball player and football player=
`P(A\cap B)=(13)/(100)=0.13`

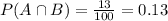
We have to find the probability that athlete is either a football player or a basketball player.

It means we have to find
`P(A\cup B)`

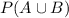
We know that

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

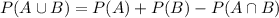
`P(A\cup B)=0.40+0.59-0.13=0.86=0.86* 100=`86%

Hence, the probability that the athlete is either a football player or a basketball player=86%