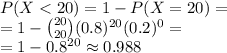Question

A university claims that 80% of its basketball players get degrees. An investigation examines the fate of all 20 players who entered the program over a period of several years that ended six years ago. Of these players, 11 graduated and the remaining 9 are no longer in school. If the university's claim is true, the number of players among the 20 who graduated should have the binomial distribution with n = 20 and p = 0.8. Use the binomial probability formula to answer the question, What is the probability that not all of the 20 graduate?

Answer 1

The probability of not all players graduate in approximately 0.988.

Explanation:

Let's define,

`X` = "Number of players that graduated"

We know that
`X \sim Bin(20;0.8)` and the probability density function for a binomial random variable is:

`P(X = k) = {20 \choose k}(0.8)^k(0.2)^(20-k)`, with
`k \leq 20`

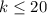
We want to know the probability that not all of the 20 graduate, in other words we want to know the probability of
`P(X < 20)`.

`P(X < 20) = 1 - P(X = 20) =\\= 1 - {20 \choose 20}(0.8)^(20)(0.2)^0 =\\= 1 - 0.8^(20) \approx 0.988`