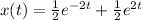Question

Equation is x"-4x=0, general solution is x(t) = C1e^-2t+C2e^2t, initial condition is x(0) = 1, x'(0)=0

Answer 1

`x(t)=(1)/(2)e^(-2t)+(1)/(2)e^(2t)`

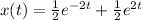
Explanation:

The given differential equation is
`x''-4x=0`

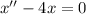
The characteristics equation is given by

`r^2-4=0\\\\r^2=4\\\\r=\pm2`

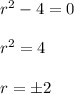
Therefore, the solution of the DE is given by

`x(t)=c_1e^(-2t)+c_2e^(2t)`

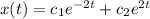
On differentiating, we get

`x'(t)=-2c_1e^(-2t)+2c_2e^(2t)`

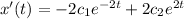
Apply the initial conditions

x(0)=1

`1=c_1e^(0)+c_2e^(0)\\\\c_1+c_2=1...(i)`

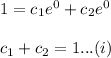
Second condition is x'(0)=0

`0=-2c_1e^(0)+2c_2e^(0)\\\\-2c_1+2c_2=0\\\\c_1-c_2=0...(ii)`

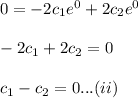
Add (i) and (ii)

`2c_1=1\\\\c_1=(1)/(2)`

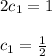
Substituting this value in (ii)

`(1)/(2)-c_2=0\\\\c_2=(1)/(2)`

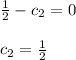
Hence, the solution of the DE is

`x(t)=(1)/(2)e^(-2t)+(1)/(2)e^(2t)`