Question

Suppose the revenue (in dollars) from the sale of x units of a product is given by R(x) = 68x? + 76% 2x + 2 Find the marginal revenue when 65 units are sold. (Round your answer to the nearest dollar.) Interpret your result. When 65 units are sold, the projected revenue from the sale of unit 66 would be

Answer 1

Answer: a) $33.98, b) $2245.05

Explanation:

Since we have given that

Revenue function is given by

`R(x)=(68x^2+76)/(2x+2)`

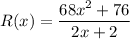
On simplifying, we get that

`R(x)=(34x^2+38)/(x+1)`

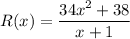
If the number of units sold = 65

We need to find the Marginal revenue.

Revenue at 65 units would be

`(34(65)^2+38)/(65+1)=\$2177.09`

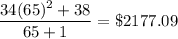
Revenue at 66 units would be

`(34(66)^2+38)/(66+1)=\$2211.07`

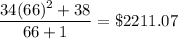
So, marginal revenue would be

`2211.07-2177.09\\\\=\$33.98`

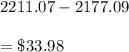
Projected revenue from the sale of 66 units would be

`2211.07+33.98\\\\=\$2245.05`

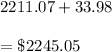
Hence, a) $33.98, b) $2245.05