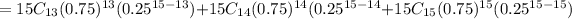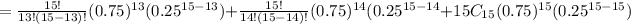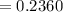Answer:
We are given that According to government data, 75% of employed women have never been married.
So, Probability of success = 0.75
So, Probability of failure = 1-0.75 = 0.25
If 15 employed women are randomly selected:
a. What is the probability that exactly 2 of them have never been married?
We will use binomial
Formula :
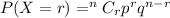
At x = 2

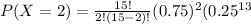
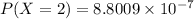
b. That at most 2 of them have never been married?
At most two means at x = 0 ,1 , 2
So,

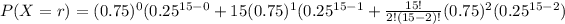

c. That at least 13 of them have been married?
P(x=13)+P(x=14)+P(x=15)