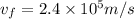Answer:
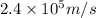
Step-by-step explanation:
We are given that
Mass of proton=
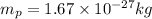
Initial speed of proton=
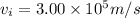

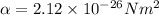
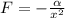
Where x is the separation between the two objects.
We have to find the speed of the proton when it is
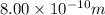 from the uranium nucleus.
from the uranium nucleus.
It means we have to find
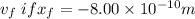
By work energy theorem
W=
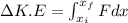
Substitute the values
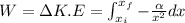
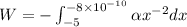
![W=\alpha[x^(-1)]^{-8* 10^(-10)}_(-5)](https://img.qammunity.org/2020/formulas/physics/high-school/iy44e442ul9qk1vhzxpnnfy0ko6f9bcfcb.png)
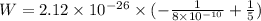
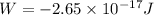
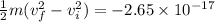
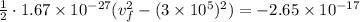
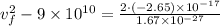
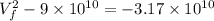
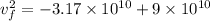
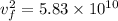
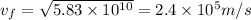
Hence, the speed of proton when it is
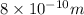 from the uranium nucleus=
from the uranium nucleus=