Question

A large rocket has a mass of 2.00×10⁶ kg at takeoff, and its engines produce a thrust of 3.50×10⁷ N. Find its initial acceleration if it takes off vertically. How long does it take to reach a velocity of 120 km/h straight up, assuming constant mass and thrust? In reality, the mass of a rocket decreases significantly as its fuel is consumed. Describe qualitatively how this affects the acceleration and time for this motion.

Answer 1

17.5 m/s²

1.90476 seconds

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration

Force

`F=ma\\\Rightarrow a=(F)/(m)\\\Rightarrow a=(3.5* 10^7)/(2* 10^6)\\\Rightarrow a=17.5\ m/s^2`

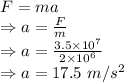
Initial acceleration of the rocket is 17.5 m/s²

`v=u+at\\\Rightarrow (120)/(3.6)=0+17.5t\\\Rightarrow t=((120)/(3.6))/(17.5)=1.90476\ s`

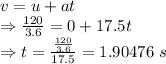
Time taken by the rocket to reach 120 km/h is 1.90476 seconds

Change in the velocity of a rocket is given by the Tsiolkovsky rocket equation

`\Delta v=v_(e)\ln (m_0)/(m_f)`

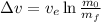
where,

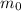`m_0` = Initial mass of rocket with fuel

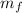`m_f` = Final mass of rocket without fuel

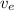`v_e` = Exhaust gas velocity

Hence, the change in velocity increases as the mass decreases which changes the acceleration