Question

When the effective interest rate is 9% per annum, what is the present value of a series of 50 annual payments that start at $1000 at the end of the first year and increase by $10 each subsequent year?

Answer 1

$1,109.62

Explanation:

Let's first compute the future value FV.

In order to see the rule of formation, let's see the value (in $) for the first few years

End of year 0

1,000

End of year 1(capital + interest + new deposit)

1,000*(1.09)+10

End of year 2 (capital + interest + new deposit)

(1,000*(1.09)+10)*1.09 +10 =

`\bf 1,000*(1.09)^2+10(1+1.09)`

End of year 3 (capital + interest + new deposit)

`\bf (1,000*(1.09)^2+10(1+1.09))(1.09)+10=\\1,000*(1.09)^3+10(1+1.09+1.09^2)`

and we can see that at the end of year 50, the future value is

`\bf FV=1,000*(1.09)^(50)+10(1+1.09+(1.09)^2+...+(1.09)^(49)`

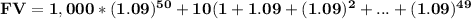
The sum

`\bf 1+1.09+(1.09)^2+...+(1.09)^(49)`

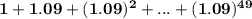
is the sum of a geometric sequence with common ratio 1.09 and is equal to

`\bf ((1.09)^(50)-1)/(1.09-1)=815.08356`

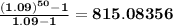
and the future value is then

`\bf FV=1,000*(1.09)^(50)+10*815.08356=82,508.35564`

The present value PV is

`\bf PV=(FV)/((1.09)^(50))=(82508.35564)/(74.35572)=1,109.616829\approx \$1,109.62`

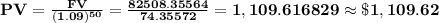
rounded to the nearest hundredth.