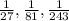ANSWER:
The next three terms of given sequence are
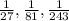
SOLUTION:
Given, series is
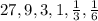
Let us find which sequence does this series belongs.
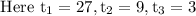
Now, let us see the common difference.

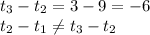
So, the series does not belong to arithmetic progression.
Now, let us see the common ratio.
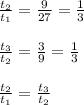
So, the series belongs to geometric progression. And common ratio(r) =

We need to find the next three terms, which are
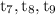
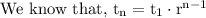
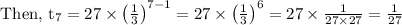
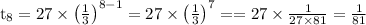
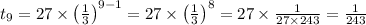
Hence the next three terms of given sequence are