Answer:
The length of VI = 4 cm
Solution:
The plot is like a quadrilateral and the fences are built on the diagonal
We know that for quadrilateral both the diagonals are in same height,
So as per the picture, GH = FI
Now we know that GV = 6.55, FV = 5.84, VH = 3.27
Hence,
GH = FI
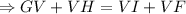
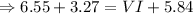

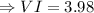
Rounding off:
- If the number that we are rounding is followed by 5 to 9, then the number has to be increased to the next successive number.
- If the number that we are rounding is followed by 1 to 4, then the number has to remain the same.
Here the number to be round off is 3.98, 9 belongs to the first category stated above. So, 3 is increased to 4.
Hence, the length of VI = 4 cm.