Question

Find the equation of the line with the slope - 2/9

and the y-intercept (0,2).
The equation of the line is...

Answer 1

The line equation with the slope
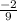`(-2)/(9)` and the y-intercept (0,2) is 2x + 9y – 18 = 0.

SOLUTION:

Given, slope of the line is
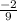`(-2)/(9)` and point on the line (0, 2).

We have to find the line equation.

As we have slope and a point, let us find the point slope form of the given equation.

Point slope form →
`y-y_(1)=m\left(x-x_(1)\right)`

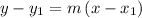
Where m is slope and
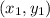`\left(x_(1), y_(1)\right)` is a point on that line

Here, in our problem,
`\mathrm{m}=-(2)/(9) \text { and }\left(\mathrm{x}_(1), \mathrm{y}_(1)\right)=(0,2)`

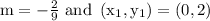
Now, we get

`\begin{array}{l}{y-2=-(2)/(9)(x-0)} \\\\ {y-2=-(2)/(9) x}\end{array}`

9(y – 2) = -2x

9y – 18 = -2x

2x + 9y – 18 = 0

Hence, the line equation is 2x + 9y – 18 = 0.