Answer:
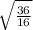
Explanation:
A rational number is one that can be expressed as a fraction.
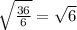
- sqrt(6) is irrational.
Therefore, top left and right and irrational.
Bottom left:

- Very obviously already in a fractional form making it rational.
Bottom right:
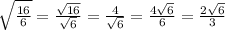
- We already established that the sqrt(6) is not rational, so this expression is also irrational.